裂纹齿轮的模态分析及诊断

　　利用振动信号直接进行模态参数识别的常用方法有Ibrahim时域法、ITD法、最小二乘复指数法、多参考点复指数法、特征系统实现法和ARMA时序分析法。本文采用ARMA时序分析法对齿轮箱振动信号进分析，进而提取系统的模态参数。在以往进行频域谱分时，常由于信号截断而引起泄露，出现旁瓣、分辨率低及信号被淹没等缺陷，而时间序列分析则与频域谱分析不同，由于时序谱是动态谱，观测数据能外延，因此不会由于观测数据的样本长度有限而产生上述缺陷。

　　3.3ARMA时序分析法原理

　　时间序列分析首先由观测数据拟合一个时序模型，然后对该模型进行分析研究，从而得出观测数据的统计特性。由于实测时间序列反映了系统工作的动态过程，因此蕴含着系统的固有特性。建立时序参数模型的目的，就是把系统本身固有的特性很好地表达出来。

　　N个自由度的线性系统激励与响应之间的关系可用高阶微分方程描述，在离散时间域内，该微分方程变成由一系列不同时刻的时间序列表示的差分方程，即ARMA时序模型方程：

　　式（1）表示响应数据序列X_t与历史值X_t-k，的关系，其中等式左边为自回归（AR）模型，右边为滑动均值（MA）模型，2N为自回归和滑动均值模型的阶次，ak、bk分别表示待识别的自回归系数和滑动均值系数，f_t-k为白噪声激励。

　　运用ARMA时序法识别模态参数首先要估算系数ak和bk的值，本文利用Prony方法对时间序列响应进行拟合获得ARMA模型的参数（可以通过调用MATLAB中的prony函数实现）。当求得自回归系数ak和滑动均值系数bk后，通过ARMA模型传递函数的表达式计算系统的模态参数，ARMA模型的传递函数为：

　　用代数方程求解法计算分母多项式方程的根：

　　求解得到的根为传递函数的极点，他们与系统的模态频率ω_k和阻尼比的关系为：

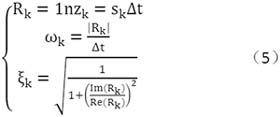
　　3.4模态参数提取结果

　　本文首先用有限元法计算了试验齿轮的前10阶固有频率，并将其作为确定实际信号带通滤波上下限的依据，然后用ARMA时序分析法对滤波后的信号进行处理，提取了不同裂纹深度的齿轮的前5阶固有频率值见表2。

表2     试验提取的固有频率值            Hz

　　从表2的模态参数识别结果来看，随着裂纹深度的增加，提取到的固有频率值也会有所降低，因此将固有频率作为齿轮裂纹故障的诊断参数是可行的。

　　4结语

　　本文提出的方法避免了传统方法诊断所带来的不便之处，并且可以有效地诊断齿轮的齿根裂纹故障诊断中。对于其它类型的故障（如点蚀、磨损等）的诊断，本文也可以为其提供一个很好的参考思路和诊断方法。