1 介绍
设计机械和结构零件时,最主要的有两个载荷源:极限载荷和疲劳载荷。极限载荷是由于载荷超过材料的屈服强度或者是超过了材料的最大强度而引起结构破坏的载荷。疲劳载荷是循环载荷,每个疲劳载荷大体上都低于材料的额定屈服强度,但达到足够次数的波动后会导致断裂。值得注意的是,除了循环载荷,还有非静态空气动力产生的载荷。另外,由于运行的风速区间大,可能会激发一些频率下的共振。一般来说,疲劳裂纹会在最大局部应力的一点或几点处形成,载荷在循环应力作用下通过材料扩展直到完全断裂。
疲劳性能受到许多变量的影响,包括载荷类型(轴向,弯曲和扭转)、载荷曲线形状、零件尺寸、零件后处理、运行温度和环境。由于因素众多,且材料非常容易受到这些因素和载荷工况微小变化的影响,对材料的疲劳寿命进行预测是很复杂的。为了计算可变载荷下零件的寿命,需要使用某种方法,把恒幅疲劳测试数据和随机应力联系起来。麦纳损伤累积法则(Palmgren-Miner cumulative damage rule)为此提供了一个简化的方法(图1)。该方法假设,在波动载荷下机械零件的破坏随着载荷循环次数线性增加,当D=1 时零件破坏(Eq.1)。此外,在变幅载荷情况下,不同应力响应бai 对应的损伤应进行累积,因此:
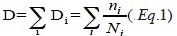 式中ni 表示载荷工况бai 载荷循环预期次数,Ni 为载荷循环бai 下发生破坏时载荷循环次数,根据Wöhler 曲线或Haigh图确定。
式中ni 表示载荷工况бai 载荷循环预期次数,Ni 为载荷循环бai 下发生破坏时载荷循环次数,根据Wöhler 曲线或Haigh图确定。
计算终身循环次数有几种方法。最简单的方法,即本文分析中所用的方法,是使用“雨流法”计算等效应力。其他方法包括最大剪应力平面确定等。
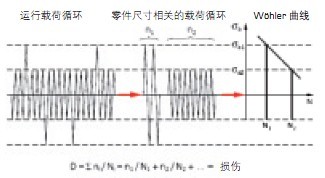
图1 根据Miner法则的载荷循环分类
 手机浏览网
手机浏览网







