因此转子飞轮受到的电磁转矩仅与iq 有关,而与id 无关。转子飞轮在z 轴方向上受到的悬浮力为上、下电机磁场吸力之差,即
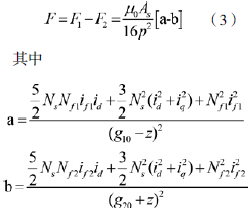
把F 在z=0,id=Id0 处进行二维泰勒展开,取常数项和一次项得
F=k1+k2z+k3idc (4)
其中k1,k2 和k3 是由式(3)中的电机的电气机械参数决定的。控制系统工作时,z 被控制在平衡位置0 附近,从而k2z ≈ 0。由于转矩与id 无关,因此可以通过调节id 中的小信号部分idc 用来控制飞轮的悬浮力F。在进行系统设计时,可以使飞轮转子重量GF ≈ k1,从而转子飞轮沿z 轴方向平动的动力学方程为
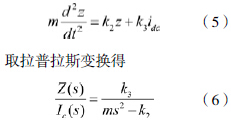
该传递函数有1 个极点位于s 平面的右半平面,系统不稳定,必须施加主动控制。采用LQR 方法设计的控制器。加入控制器后,系统的开环Bode 图如图3 中虚线所示。可见加入控制器后,系统是稳定的。
 手机浏览网
手机浏览网







