垂直轴风轮气动弹性稳定性和结构动力响应分析

    运动万程                
    为了确定旋翼——塔耦合系统的运动方程应用了Lagrange原理，为了得到动能、势能和阻尼项，必须计算桨叶上任意点的速度，经过代数转换以后，以局部坐标s。表示其速度。            
             
    从这个方程可以计算桨叶能量项目，桨叶的变形代入这个方程，能量项目就可用广义坐标表示。用Lagrange方程最后导出运动方程，这些方程是一组常系数二阶微分方程，因为垂直轴风轮结构是对称的。气动弹性稳定性和动力响应运动方程分别是：

    式中：

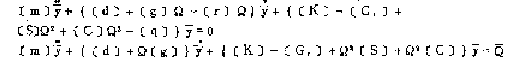
    (m)是结构质量矩阵 (d)是结构阻尼矩阵 (g)是陀螺矩阵(r)是气动阻尼矩阵(k)是结构刚度矩阵(G)是重力矩阵(S)是几何刚度矩阵
(C)是离心力矩阵 (q）是气动刚度矩阵            
    而y=(△e、．h0 2、qi、SKi]’，广义力  Q来源于气动力，重力和离心力，并由下列表  达式得到；Q={Q。+一Q。)6u。／6ydr式中Q。和Q。分别为气动力和重力，以局  部坐标Ss表示，U’是桨叶上一点的变形矢量。            
    结  果
    上述描绘的理论模型已程序化了，并用于一些可用风轮的稳定分析，其中获得使用证书的风轮是安装在荷兰FOKKER的PIONEElR I风轮。该风轮旋翼高度为15m，直径为14．92 m，桨叶形状为tropos kien而弦长为O．75m的垂直轴风轮，转速变化在低风速时为25r／min，在风速1Gm／s时为50r／min，在风速18m／s，。输出45kW。本文以PIONEER I风轮作为铡算，证实了方法的可用性。
    结    论